Задача 1. O лифтах (1 сек.)

Рассматриваем N-этажный дом. В нем всего один подъезд и на этажи людей доставляют M лифтов. Все лифты имеют постоянную скорость движения, равную 1 этаж в секунду. Время остановки лифта на этаже равно T секундам. Лифт не может перевозить одновременно более Q человек. На каждом этаже есть только две кнопки для вызова лифта v одна вверх и одна вниз. На первом и последнем этажах v по одной кнопке: вверх и вниз, соответственно.

Нужно написать программу, определяющую минимальное время ожидания лифта пассажиром, который на этаже F нажал одну из кнопок, причем считать, что других пассажиров, ожидающих лифта, нет. Следует заметить, что если через этаж, на котором стоит человек, проходит лифт, едущий в противоположную сторону, то он данного пассажира брать не будет. Если лифт пустой, он стоит на том этаже, где его покинул последний пассажир.

Формат ввода:

В первой строке входного файла input.txt записаны четыре целых числа через пробел N, M, Q, T, где 1 £ N, M £ 255 и 1 £ Q, T £ 10.

Вторая строка содержит информацию о пассажире - это два числа, первое из которых - номер этажа F, а второе - номер нажатой кнопки (1 v вверх, 2 - вниз)

Следующие М строк описывают состояния лифтов. Каждая строка соответ-ствует одному лифту. Первое число здесь - это номер этажа, на котором находится лифт, затем два числа задают его состояние движения. Возможны следующие варианты:

1 1 - лифт идет вверх, 1 2 - идет вниз, 0 K - стоит K секунд.

Далее дается загруженность лифта (количество человек, находящихся в лифте), и, наконец, описывается план остановок: количество следующих остановок - целое число R, за которым следуют R (0 £ R) пар чисел. Первое число в паре v это номер этажа, где лифт должен остановиться, а второе - количество пассажиров, едущих до этого этажа (остановки могут быть неупорядочены). Количество пассажиров, которых надо высадить, всегда больше нуля. Если лифт идет вверх, то среди остановок не может быть этажей, расположенных ниже этажа, на котором находится лифт в данный момент. Аналогично, если лифт направляется вниз, то в списке остановок могут присутствовать только номера этажей, расположенных ниже текущего.

Формат вывода:

В выходной файл output.txt записывается одно целое число v минимальное время ожидания лифта.

Пример.

input.txt: ================================ Комментарии:

9 4 5 10 =========================== 9 этажей, 4 лифта, вместимость v 5 человек, время стоянки v 10 секунд

5 2======================================= пассажир на 5 этаже нажал кнопку вниз

7 0 2 5 3 4 3 2 1 1 1 лифт на 7 этаже стоит 2 секунды, в нем находится 5 человек, ему нужно сделать 3 остановки: на 4 этаже высадить 3 человек, на 2-м v одного, и на 1-м тоже одного пассажира

4 1 1 2 1 6 2================== лифт на 4 этаже идет вверх, везет 2 человек, нужно сделать 1 остановку на 6 этаже и высадить этих двоих

4 1 2 3 2 3 2 2 1========= лифт на 4 этаже идет вниз, везет 3 пассажиров, нужно сделать 2 остановки, на 3 этаже высадить двоих человек, на 2-м v одного.

1 0 0 0 =========== лифт стоит на первом этаже 0 секунд, он пустой, у него нет плана остановок.

output.txt:

13

Задача 2. Даты (5 сек.)

С целью проверки гипотезы академика Фоменко о LНовой хронологии_ было решено проверить датировку документов городского архива г. Урюпинска. При этом выяснилось, что датировки документов могут содержать неоднозначности. Перед Вами стоит задача написать программу, по возможности разрешающую эти неоднозначности.

Формат ввода:

Входной файл input.txt состоит из не более чем 1000 строк, длина каждой строки не более 255 символов.

Строка состоит из трех чисел, разделенных неалфавитно-цифровыми символами ASCII. Первые два числа могут означать день и месяц или месяц и день. Третье число обозначает год, обозначаемый одной, двумя или четырьмя цифрами. Даты ранее 1000 года н.э. во входном файле отсутствуют.

Формат вывода:

Для каждой строки входного файла в выходной файл output.txt необходимо вывести строку следующего вида:

* если числа входной строки могут быть однозначно проинтерпретированы как дата григорианского календаря, вывести эту дату в формате dd/mm/yyyy;

* если они могут быть проинтерпретированы как несколько разных дат, вывести все эти даты в календарном порядке (более ранняя дата идет первой) через запятую;

* если они не могут быть проинтерпретированы как дата григорианского календаря, вывести "No Date".

Годы, обозначаемые одной цифрой, следут интерпретировать как 2000-й год или годы XXI столетия. Годы, обозначаемые двумя цифрами, следует интерпретировать как 1900 год или годы XX столетия.

Пример.

input.txt:

0 / 0/ 0

29/ 02/ 1900

29/02/0

01/01/1

01 - 02 - 01

output.txt:

No Date

No Date

29/02/2000

01/01/2001

02/01/1901, 01/02/1901

Задача 3. Об авиакомпании (5 сек.)

Имеется карта авиасообщений компании NABLA. Для каждого города известно расписание прибытия и вылетов самолетов этой авиакомпании. Также известно расстояние и стоимость билета между городами, для которых есть прямой рейс. Стоимость билета с посадкой в промежуточных пунктах в авиакомпании NABLA дешевле, чем стоимость прямых (без посадки) билетов. Скидка, получаемая при каждой промежуточной посадке, равна 0.01*S, где S - уже налетанные в таком рейсе мили, то есть если Вы летите из T0 в T3 через T1, T2, то за посадку Т1 получаете скидку на сумму в 0.01 * Расстояние(Т0, Т1), в Т2 - на сумму 0.01 * (Расстояние( Т0, Т1 ) + Расстояние (Т1, Т2)). При посадке в уже посещенный город все скидки теряются.

Напишите программу, которая определяла бы самый дешевый путь между заданными городами, укладывающийся в заданные временные рамки.

Формат ввода:

Входной файл input.txt содержит следующую информацию:

количество городов (не более 20-ти, имя города не более 25 символов, альтернативная кодировка), количество рейсов; карту - пары городов, между которыми есть прямое сообщение, со стоимостью, расстоянием и временем перелета; время, отведенное на перелет (не более 24-х часов); начальный и конечный пункты; расписание рейсов в каждом городе.

Формат вывода:

В выходной файл output.txt вывести стоимость перелета. Если нет маршрута, укладывающегося в заданное время, вывести -1.

Пример.

input.txt:

3 3

Москва Сан-Франциско 970 11350 13.00

Москва Нью-Йорк 620 8500 8.45

Нью-Йорк Сан-Франциско 425 3800 5.00

15 часов

Москва Сан-Франциско

Москва:

=Прилет из: Сан-Франциско 4.30 am

=Прилет из: Нью-Йорк 9.15pm

=Вылет в: Сан-Франциско 7.20pm

=Вылет в:Нью-Йорк 5.15am

Нью-Йорк:

=Прилет из: Сан-Франциско 3.14pm

=Прилет из: Москва 6.00am

=Вылет в: Сан-Франциско 7.10am

=Вылет в: Москва 4.30 am

Сан-Франциско:

=Прилет из: Нью-Йорк 3.10 pm

=Прилет из: Москва 9.20 pm

=Вылет в: Нью-Йорк 1.14 pm

=Вылет в: Москва 4.30 am

output.txt:

960

Задача 4. Азбука Морзе (1сек.)

Некая флотилия с целью максимально увеличить скорость передачи сообщений между своими кораблями решила оснастить все свои корабли новой азбукой Морзе. Для этого был объявлен конкурс проектов. Представители флотилии дают Вам, как одному из претендентов, тестовое сообщение, по которому надо разработать новую азбуку, обеспечивающую минимальное время передачи этого сообщения. До получения заказа Вы разглашаете только время передачи тестового сообщения с помощью новой азбуки.

В азбуке каждому символу должна соответствовать уникальная комбинация из точек и тире длиной не более 5-ти знаков. Строчные и прописные буквы передаются одним кодом. Известно также, что отношение скоростей передачи точки и тире равно 1:3.

Формат ввода:

Входной файл input.txt содержит текст из латинских букв, знаков препинания и десятичных цифр. В файле не более 5000 символов.

Формат вывода:

В выходной файл output.txt вывести время передачи текста из входного файла на найденной Вами азбуке. Скорость передачи точки считать равной 1, время на паузы не учитывать.

Пример.

input.txt:

aaaabB

output.txt:

8

Задача 5. Деревья (3 сек.)

При разработке системы поддержки бизнеса для компании, занимающейся оффшорным программированием, возникла задача интеграции системы документооборота с Microsoft Project. И система документооборота, и MSP, поддерживают иерархические (древовидные) структуры задач и подзадач и допускают изменения в структуре дерева. Интеграция состоит в репликации этих древовидных структур из системы документооборота в MSP и обратно.

Одна из подзадач репликации состоит в следующем:

Дан древовидный граф, узлы которого имеют уникальные идентификаторы. Мы создаем две копии (реплики) этого графа, сохраняя взаимно-однозначное соответствие между узлами, имеющими одинаковые идентификаторы. Затем мы начинаем редактировать каждую из реплик, перенося, удаляя и добавляя узлы. При этих операциях граф всегда остается древовидным и его исходная корневая вершина остается корневой. Затем мы осуществляем репликацию (слияние) копий графа по следующим правилам:

• в результате репликации обе копии должны стать идентичными;
• редактированием вершины считается ее удаление или перенос по иерархии (изменение родительской вершины);
• если вершина подвергалась изменению только в одной реплике, это изменение должно быть отражено в результирующем графе;
• если вершина подвергалась редактированию в обоих копиях, возникает конфликт репликации. Правила разрешения конфликта таковы:
• если в обеих репликах узел был удален, то он удаляется;
• если в одной из реплик узел был удален, а в другой - изменен, удаление игнорируется.;
• если в обеих репликах произошел перенос (не удаление), то используется значение из первой реплики;
• если в результате применения предыдущих правил возникает цикл, он разрывается так, чтобы вершина с лексикографически наименьшим идентификатором оказалась в вершине образующегося поддерева.

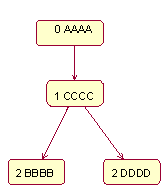
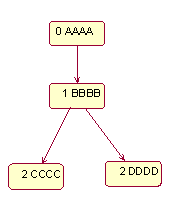
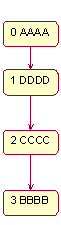
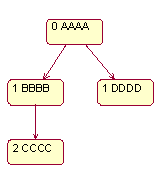
Формат ввода:

Во входном файле input.txt даются две реплики древовидного графа в линеаризованной прямым обходом форме. Каждый узел описывается одной строкой, состоящей из трех полей, разделенных пробелами. Первое поле содержит глубину узла (0 для корневого узла). Родителем узла глубины N считается ближайший к нему сверху узел глубины N-1. Второе поле содержит признак, модифицировался ли узел в данной реплике (0 для неизмененных, 1 для измененных, 2 для удаленных). Третье поле содержит алфавитно-цифровой идентификатор узла (строку длиной 8 символов). Каждая реплика начинается с корневого узла.

Формат вывода:

В выходной файл output.txt вывести объединенный граф в том же формате, но без признаков модификации узлов. Потомки каждого узла должны быть лексикографически отсортированы.

===========

Ограничения:

Количество узлов не превосходит 100.

Пример.

input.txt:

0 0 AAAA

1 1 BBBB

2 1 CCCC

3 0 DDDD

0 0 AAAA

1 1 DDDD

2 1 CCCC

=3 0 BBBB

output.txt:

0 0 AAAA

1 1 BBBB

2 1 CCCC

1 1 DDDD

Пояснение к примеру:

Исходный граф:

2 реплики:

==== ===========

Результат:

Задача 6. О командировке (3 мин.)

Представитель фирмы Микронова отправлен в служебную командировку. Он знает, сколько рабочих дней нужно провести в каждом городе, какие города соединены авиационным рейсом, расписание и стоимость этих рейсов, и стоимость проживания в каждом из городов. Работа начинается на следующий день после прилета и заканчивается в день перед вылетом. По субботам и воскресеньям никто не работает. Командировка начинается из Новониколаевска и заканчивается в нем же. В каждом городе можно побывать только один раз. Отсчет дней командировки начинается с понедельника. Нужно минимизировать затраты на командировку.

Формат ввода:

Во входном файле input.txt даются количество городов (не более 7), названия городов (по одному на строчке, длина имени не более 25 символов, альтернативная кодировка), стоимость проживания в каждом из них и число дней на работу (не более 16 в каждом городе). Кроме того, дана база данных авиационного расписания в форме: номер города вылета, номер города прилета, стоимость, дни рейсов. Если дни рейсов не указаны, самолет летает ежедневно. Все стоимости не более 30000.

Новониколаевск имеет номер 0 и в базу городов не включен.

Формат вывода:

Первая строка выходного файла output.txt должна содержать одно целое число - минимальные затраты на командировку. В последующие сроки необходимо вывести расписание командировки в форме:

Город день

Город день

Если нельзя составить расписание, удовлетворяющее условиям, вывести 0.

Пример.

input.txt:

2

Нижний Новгород 500 4

Москва 1500 5

0 2 4000

0 1 3000 1 3 5

1 0 2800 2 4 6

2 0 4500

1 2 1000

2 1 1000

output.txt:

18300

Москва 7

Нижний Новгород 13

Новониколаевск 20

Задача 7. Экспонента (3 сек.)

Вычислить exp(n), где n - длинное целое число (long int).

=Формат ввода:

Во входном файле input.txt дается n.

Формат вывода:

В выходной файл output.txt вывести результат в форме двух целых чисел. Первое число - степень десятки в представлении данного числа в форме a*10^K, где 0.1< a £1.0. Второе - десять старших значащих цифр числа a.

Пример.

input.txt:

1

output.txt:

1

2718281828

Задача 8. О диете (10cек.)

Чтобы похудеть, некоторые люди начинают усиленно заниматься спортом, а некоторые изнуряют себя многочисленными диетами. Особенно жители Америки старательно отслеживают, сколько калорий содержит тот или иной продукт, который они покупают.

Для того, чтобы не превысить количество потребляемых с пищей калорий, человеку необходимо вести сложные подсчеты. А так как низкокалорийные продукты дороги по сравнению с теми, которые обычно употребляют в пищу, то на составление меню может уйти достаточное количество времени.

Число калорий K, которое может содержаться в съедаемых за день продуктах, заведомо известно.

Написать программу, которая по предлагаемому набору выбирала бы наименее калорийные продукты. При одинаковом количестве калорий, содержащихся в разных продуктах, брать тот продукт, который дешевле.

Таким образом, меню составляется из расчета К_5 калорий на день из продуктов наименьшей стоимости.

Формат ввода:

В первой строке входного файла input.txt содержатся два целых числа 0< K £3000 и 0<S£300, которые соответствуют необходимому числу калорий в день и сумме, в которую закупка продуктов должна уложиться.

Во второй строке - число 0< N £60 - количество предлагаемых продуктов.

В последующих N строчках содержится название продукта не более чем из 10 символов (альтернативная кодировка). Через пробел число 0< C £100, которым определена стоимость минимальной расфасовки данного продукта, и еще через пробел число калорий в минимальной расфасовке.

Формат вывода:

В выходной файл output.txt вывести минимальную сумму, в которую может обойтись закупка продуктов, необходимых для соблюдения диеты.

Пример.

input.txt:

795 15

9

мясо 6 120

салат 12 300

хлеб 4 550

рыба 3 100

мин. вода 6 20

фрукты 10 70

овощи 7 100

молоко 5 150

шоколад 14 450

output.txt:

12

Задача 9. Туристический маршрут (5 сек.)

С группой горных туристов, проходящей по одному из маршрутов, случилось непредвиденное обстоятельство. Перевал,= через который они должны были пройти, оказался под завалом. В связи с этим= срочно понадобилось найти новый путь от точки, в которой прервался запланированный маршрут, до конечного пункта. Чтобы хватило оставшихся у группы продуктов, решено было минимизировать количество дней, за которое можно добраться до намеченного пункта.

На карте, имеющейся у туристов, пункты, через которые можно прокладывать= маршрут, занумерованы числами ( £ 100 ) и указано количество дней, необходимых для преодоления расстояния между каждой парой пунктов.

Напишите программу, вычисляющую минимальный по количеству дней новый маршрут для туристической группы.

Формат ввода:

В файле= input.txt содержится следующая информация:

T в первой строке целое число K £ 100 v количество пунктов, через которые может проходить путь;

T во второй строке через пробел записаны номер= пункта на карте, от которого необходимо проложить новый путь и номер пункта, в который группа туристов= должна прийти.

T в каждой следующей= строке до конца файла располагаются= три целых числа: первые два v номера пунктов, между которыми есть прямое сообщение, третье число= v= количество дней пути между ними.

Формат вывода:

В файл output.txt выдать целое число v минимальное количество дней, за которое можно пройти новый маршрут. Если такой путь найти нельзя, то вывести -No-.

Пример:

input.txt:

6

1 7

1 2 2

1 3 1

3 6 1

3 7 2

6 7 1

2 4 1

output.txt:

3